Problems tagged with "diagonal matrices"
Problem #44
Tags: linear algebra, quiz-03, diagonal matrices, eigenvectors, lecture-04, linear transformations
The figure below shows a linear transformation \(\vec{f}\) applied to points on the unit circle. Each arrow shows the direction and relative magnitude of \(\vec{f}(\vec{x})\) for a point \(\vec{x}\) on the circle.
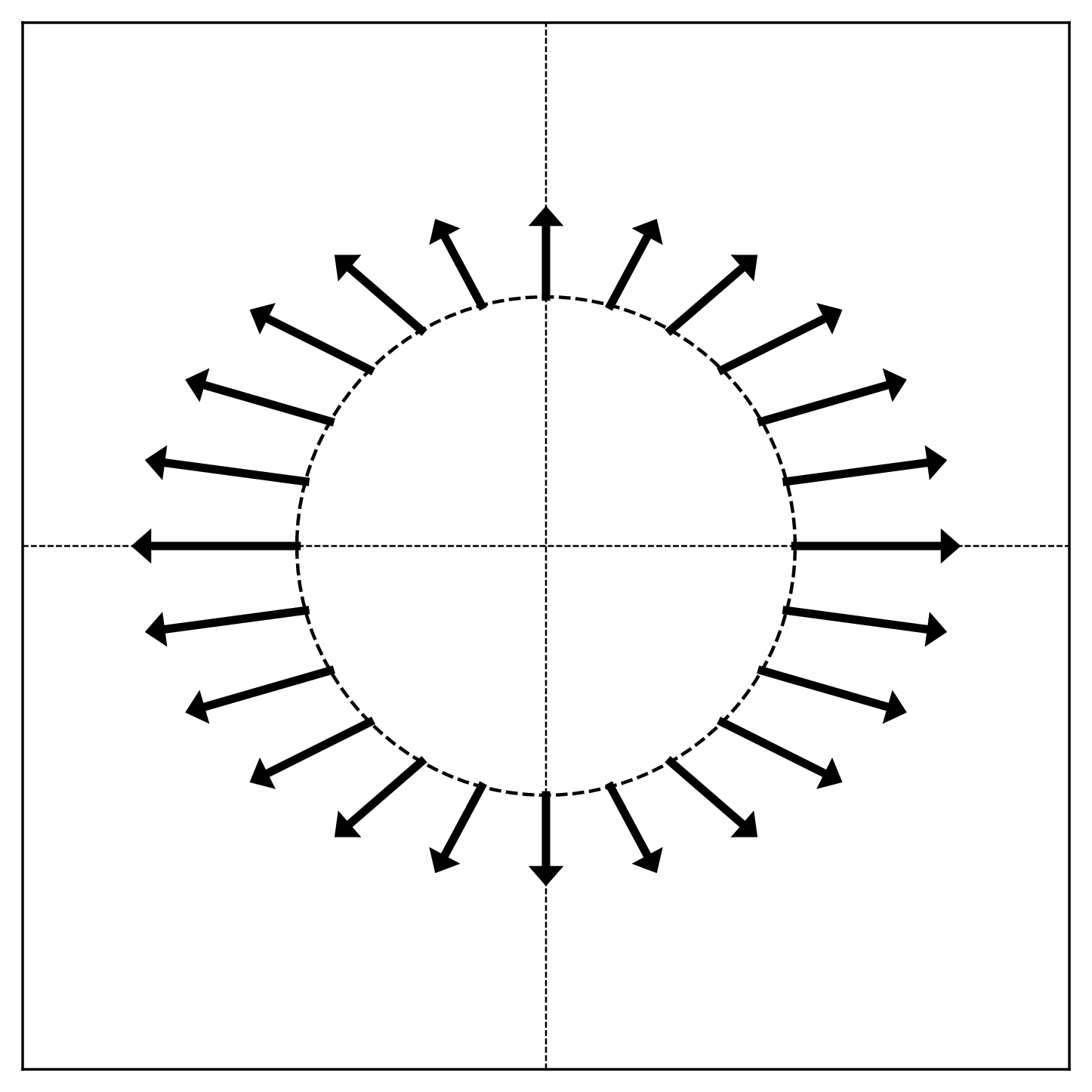
True or False: The matrix representing \(\vec{f}\) with respect to the standard basis is diagonal.
Solution
True.
A matrix is diagonal if and only if the standard basis vectors are eigenvectors. In the visualization, eigenvectors correspond to directions where the arrows point radially (directly outward or inward).
Looking at the figure, the arrows at \((1, 0)\) and \((-1, 0)\) point horizontally, and the arrows at \((0, 1)\) and \((0, -1)\) point vertically. This means the standard basis vectors \(\hat e^{(1)} = (1, 0)^T\) and \(\hat e^{(2)} = (0, 1)^T\) are eigenvectors.
Since the standard basis vectors are eigenvectors, the matrix is diagonal in the standard basis.